ネットから脱出して旅に出る。
群れから離れて隠れ家で読書する。
仕事に疲れて自然食に還る。
年号が変わるまで天皇制を刷り込まれる時、
辺野古を忘れている限り、
どこへでもありふれた誰もが逃亡だ。
焚火で暗くなる月よりも
裏庭の栗の木に登って
まぎれた春風を受信する。
裏庭の栗の木
月別アーカイブ: 2019年4月
テンセグリティは構造の最終形態
テンセグリティは構造の最終形態である。
免震、制震、耐震装置は不要だ。
すべて付加的な装置で住宅を高価にさせることをだれも疑わない。
航空機のような動く構造は建築家は設計できない。
彼らは土地資本主義の奴隷だからテンセグリティをもっと危険な構造と考えている。
免震、制震、耐震装置はすべて付加的で高額なパーツ
テンセグリティ構造はこれらの装置を陳腐化する
正4面体の動的な空隙システム
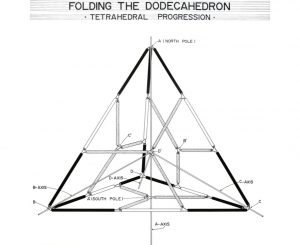
4つの面の2面角が一定に互いに交差する時、
正4面体の空隙が形成される。
その空隙と相補的な正8面体の空間も同時的に形成される。
正4面体の空隙が動的だから
黄鉄鉱には、八面体の相補的な4面体は形成されない。
空間充填には実と虚の相補的システムが存在する。
2面角が一定に互いに交差して4面体を形成する時、
八面体の相補的な4面体は形成されない。
黙々と仕事をする時が訪れる
こどもは遊びに夢中になれるばかりか、
無心になれる遊びを探す能力がとても高い。
私にも他人を説得するよりも
黙々と仕事をする時が訪れる。
それは動機が強くなければ出来ないからではなく
無心になれる目的を発見する力が生得的だからだ。
動機が破壊されるシステムの奴隷にはその無心さがない。
こどもでさえも。
4つの面の2面角が一定に互いに交差する時、正4面体の空隙が形成される。
その空隙と相補的な正8面体の空隙も同時的に形成される。
これ以上の無垢なシステムがあるだろうか。
正4面体の空隙は静止的でも固体的でもない。
SYNERGETICS RBF 1975
Intercomplementary transformings
惑星の公転周期の2乗は軌道長半径の3乗に比例する。
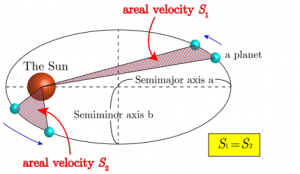
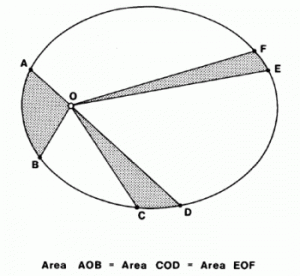
惑星が太陽を焦点の一つとする楕円軌道上を動く時、
ケプラーの第二法則(面積速度一定の法則)が生まれる。
観察からは発見できない原理の発見方法は知識ではない。
ケプラーの第二法則を証明できる知識は理解できるが、
その証明方法のなかに原理の発見方法は含まれない。
惑星が太陽を焦点の一つとする楕円軌道上を動く時、
ケプラーの第二法則(面積速度一定の法則)が生まれる。
ケプラーの第二法則は楕円軌道の離心率に依存しない。
脳のゴミを排除しても無秩序は変わらない
人間の脳のゴミは、
理解よりも深い睡眠によって排除できる。
脳は睡眠によって情報を整理するが
無秩序は変わらない。
知識自体は互いに無関心なので
経験によって統合されないかぎり
無秩序は身体から排除できない。
季節と無関係に焚火をする時、
私は太陽からのエネルギー循環に同期できる。
惑星が太陽を焦点の一つとする楕円軌道上を動く時、
ケプラーの第二法則(面積速度一定の法則)が生まれる。
「シナジェティクスの問題」
シナジェティクス原理を探査するための
モデル言語の生成装置は
人間の脳には備わっている。
その経験が知識を容赦なく破壊していく時、
「シナジェティクスの問題」は
個性や創造性開発のノウハウなどとは無関係に発生する。
学校に行けば行くほど無力になる現実を理解できる。
FIVE TETRA シナジェティクス研究所 梶川泰司 制作 1988年
「シナジェティクスの問題」
書物は消滅する。
映像も消滅する。
それでもモデル言語が生成される時
高い知性は獲得される。
これが「シナジェティクスの問題」だ。
私はいまでも子どもと一緒に
シナジェティクスを探査している。
「創造性」は知識に依存しない。
「創造性」は間違った概念だから。
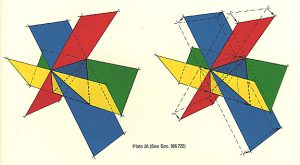
シナジェティクスは準結晶を構成するモジュールがオクテットトラス構造を発見した。1990
3種の金属からなる準結晶
モデル言語はデザインできない
モデル言語はデザインできない。
発見される以外に生成されない。
シナジェティクスモデルは
すべてモデル言語の多層的な視覚化なのである。
幾何学のように静止的ではない
シナジェティクスは時間を含む。
総三角形化されたオクテットトラスでさえ折りたたみできる。
展開型テンセグリティ構造として。
Stabilization of Tension in Tensegrity Column
SYNERGETICS RBF 1975
多頂点体（Polyvertexion）の構造的距離
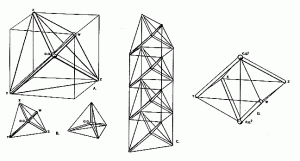
思考言語がモデル言語に接近すれば、
構造と意味がモデルに変換される。
その逆から、
反対称性を備えた自然の完全な相補性さえも生成される。
モデル言語は生成文法だ。
自然が構造的距離を最短にする計算方法は
正12面体状多頂点体（Polyvertexion）を
正4面体状多頂点体（Polyvertexion）に変換する場合だ。
20多頂点体（Polyvertexion）シナジェティクス研究所 梶川泰司 作成 1989
