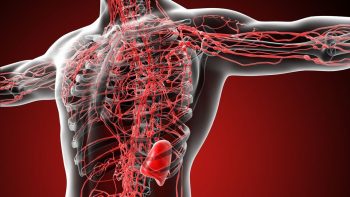
フリーダイバーのジャック・マイヨールが100mを超える潜水記録を樹立できた時、
すべての血管と毛細血管の血液が圧縮され難い原理によって
テンセグリティの圧縮材として機能させた可能性を思い描く。
血管からなる圧縮材ネットワークは非対称テンセグリティを形成する。

血管からなる非対称テンセグリティ

ブロックチェーンの概念図が球状ではないことが
ブロックチェーンのリアルな構造安定性を
決定的に視覚化できていない。
テンセグリティ構造と比較するとブロックチェーンの
P2Pとモジュールとのシナジー効果が
相似律的に4次元的に物質化されていることが分かる。
人間と情報の中央管理は時代遅れだ。

ロックチェーンの概念図は球状ではない

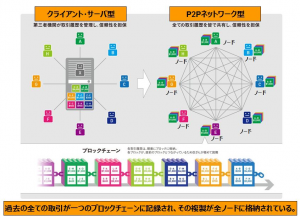
ブロックチェーンの優れた機能は
P2Pのシステムに対して情報をモジュール単位にすることによって
データの信頼性を高める方法にある。
しかし、ブロックチェーンの概念図はまだ2次元的だ。
モジュールからなるP2Pはテンセグリティを起源とする。
その構造とパターン以上の柔軟な強度は存在しない。

外力分散機能を備えたテンセグリティはもっとも破壊されにくい構造
SYNERGETICS　RBF　1975

空気は圧縮されやすい。
消化中の消化ホースは、岩のように固体的なのは
水は圧縮されにくいからだ。
植物の導管には水が満たされて無数の消化ホースが形成されている。
枯れ木が、折れやすいのは導管内部の水がなくなり
導管が空洞化して空気が入ったからである。

カボチャの導管内の水分は螺旋状の細胞壁で囲まれる

構造が安定している場合、
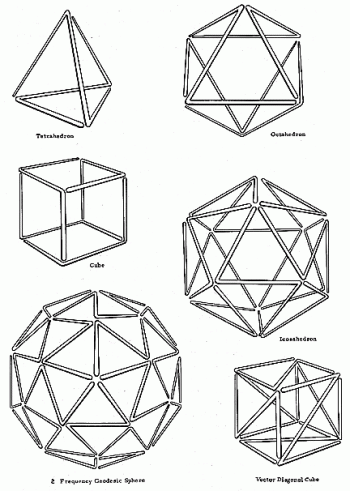
その総ストラット数はつねに6の倍数から形成されている。
正4面体の稜線数6を単位とした整数倍である。
正8面体も正20面体も正4面体の稜線数の整数倍である。
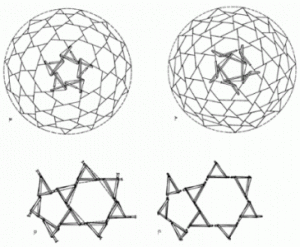
最小限の三角形のスパイラルまたはヒリックスは
Ｚ型の互いの鏡像から形成される。

Triangular Spiral Events From Polyhedra. SYNERGETICS RBF 1975

物理的現象は経験できる。
つねに特殊な経験として再現できる。
知性はそれらの異なる物理的経験を分析統合できる。
その逆は不可能である。
局所的な経験は知性に対して不可逆的である。
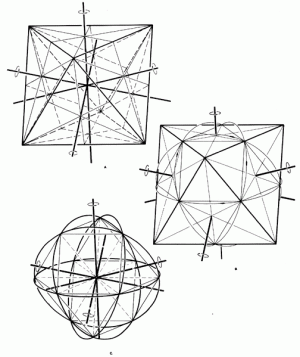
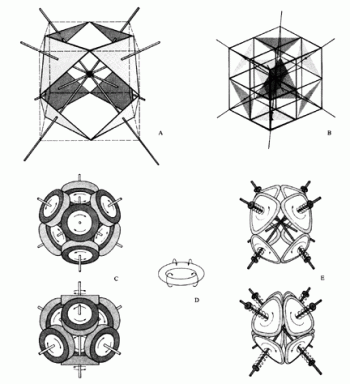
ベクトル平衡体だけから
誰も4つの回転軸上のすべての三角形の回転運動を思いつかない。
視覚的学習さえも特殊な経験段階である。

4つの回転軸のあるベクトル平衡体 SYNERGETICS RBF 1975

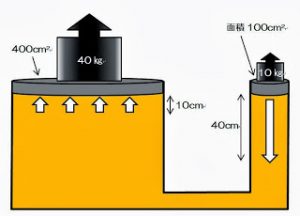
消化中の消防ホースは石のように固体的に変化する。
水は固定的液体である。
水は空気に比べ圧縮性がないので昇圧できる。
水は圧縮され難いのは、
パスカルの原理「密閉容器中の流体は容器の形に関係なく
単位面積当たりの圧力をそのままの強さで
流体の他の全ての部分に伝える」
と異なる原理だ。

パスカルの原理

真の沈黙は、全体的パターンと局所的なパターンとの関係の認識によって
メタフィジカルなノウハウ体系が物理的体系に変換された直後にはじめて訪れた。
それはテンセグリティ構造を
暴風雨圏内で使用される生活器に最適化した実験時の
内部空間の広がりと静けさに相似している。

テンセグリティモデル　
シナジェティクス研究所　制作　テンセグリティ・ジョイントデザイン　梶川泰司

ジョイントにはストラットを拘束する機能があるが
同時に角度的自由度を向上させる機能もある。
構造の安定化はジョイントにではなく構造のパターンに求められる。
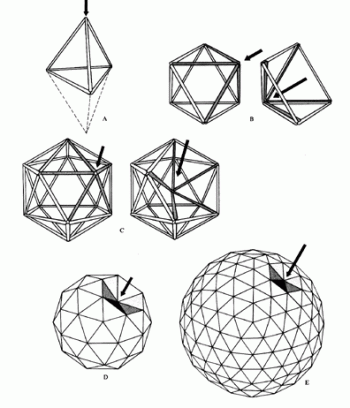
ジオデシック構造の真の安定化は総三角形化にあって
重量とコストの上昇を伴うジョイントの剛性化には求めない。

SYNERGETICS　RBF 1975
The geodesic spheres (D and E) exhibit “very local” dimpling as the frequency increases, suggesting much less resistance to concentrated loads but very high resistance to distributed loads.

私は「知識はあるが論文が書けない」
又は「経験はあるが論文が書けない」タイプでもない。
「直観を言語化できない」タイプだった。
直観の言語化には膨大な経験が必要だ。
直観的モデリングはやがて経験に変換される。
暗黒時代から逸脱する言語は
シナジェティクスの動的な直観幾何学にある。

Four-great-circle Systems of Octahedron and Vector Equilibrium: Symmetry
SYNERGETICS　RBF 1975